Interactive mathematical visualisation applications for meditation, consciousness expansion, and neuromodulation. These apps are the creative source of all Psyvector geometric art.
Wave Harmony Space is a sanctuary of moving mathematics, interactive applications that guide the mind toward stillness through evolving geometry, harmonic oscillation, and contemplative play. Each tool is designed for meditation, focus, and gentle shifts in consciousness. This is also where all Psyvector geometric art originates
The Apps
Interactive Tools for Inner Exploration
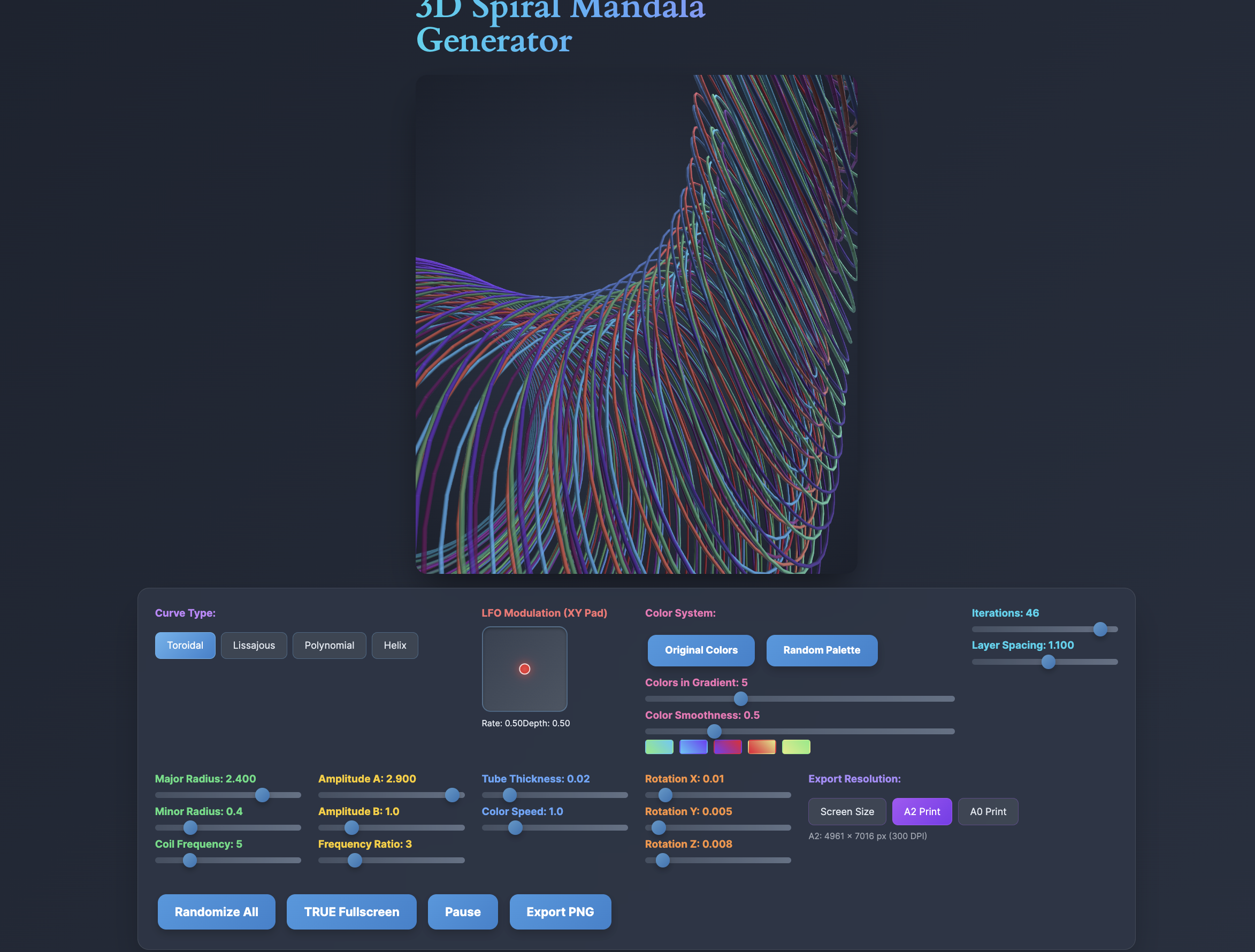
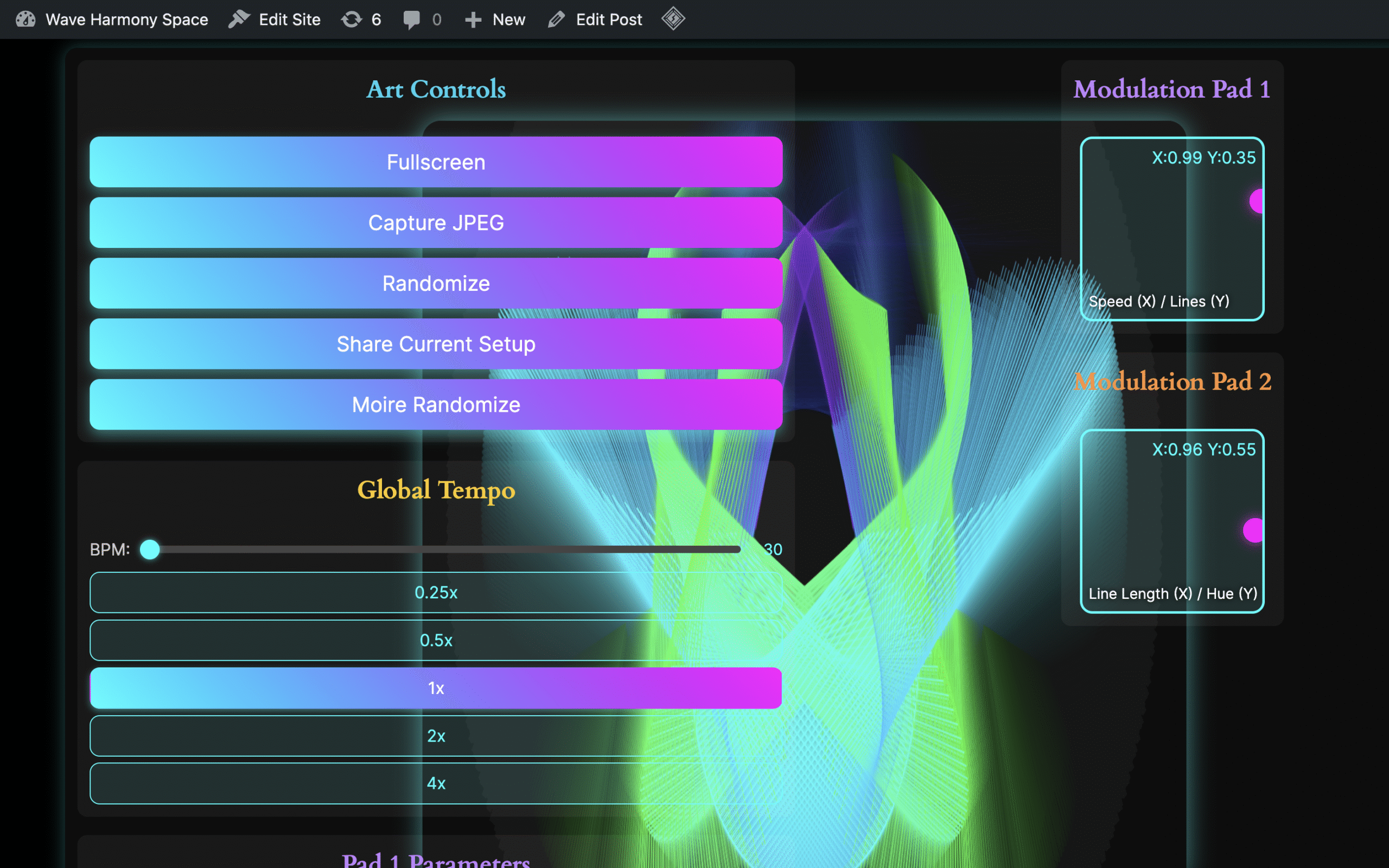
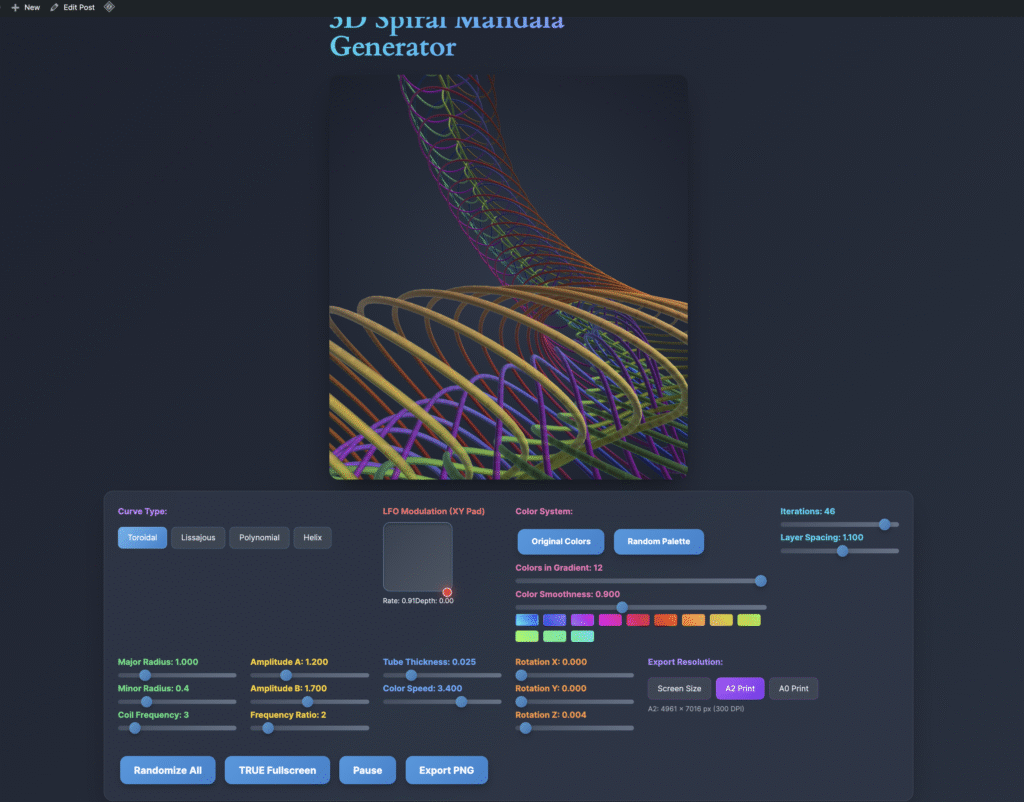
Each application in the Wave Harmony Space suite draws on WebGL shaders, physics simulations, and algebraic formulae to create fluid, evolving visual fields. Users interact through intuitive XY pad controls and parameter sliders, shaping the geometry in real-time — an active form of meditation rather than passive observation. The interface design prioritises sensory-sensitive accessibility, avoiding harsh stimuli while offering genuine depth for extended contemplation. Whether exploring Hopf fibrations, strange attractors, or sacred geometry generators, visitors are invited into fullscreen immersion where mathematics becomes a doorway to altered states.
Beyond their function as wellness tools, these applications represent a living laboratory for visual research. Every app in the suite has been developed through AI-assisted “Vibe Coding” — a creative methodology that translates decades of experience in sonic mood engineering into the visual domain. The same instincts that once shaped dancefloor atmospheres now guide the tuning of oscillation speeds, colour harmonics, and geometric complexity. Wave Harmony Space is where this exploration happens in public, inviting others to participate in the same mathematical territories that feed the Psyvector art collection.

Hopf Fibration Explorer • Sacred Geometry Generator • Fractal Meditation Tools • Strange Attractor Visualizers • Harmonic Animation Suite
The Approach
AI-assisted “Vibe Coding” • XY pad interfaces • BPM synchronization • High-resolution export for projection and print • Smooth meditative animations
Visit waveharmony.space

THE MATH
Mathematical Foundations of Wave Harmony Space
Core Mathematical Systems
Lissajous Curves & Harmonic Ratios I extensively use Lissajous figures – the interference patterns created when two sinusoidal waves interact at different frequencies. These emerge from parametric equations like x = A·sin(aωt + δ), y = B·sin(bωt), where the ratio a:b creates distinct harmonic relationships. When I use ratios like 3:2 (perfect fifth), 4:3 (perfect fourth), or more complex ratios like 8:5, I’m encoding musical consonance directly into geometric form – the same mathematical relationships that create harmony in sound create visual harmony in my animations.
Strange Attractors & Chaotic Systems I employ chaotic dynamical systems like the Lorenz attractor, Rössler attractor, and others. These are systems of differential equations that create bounded yet unpredictable trajectories – order within chaos. The Lorenz system (dx/dt = σ(y-x), dy/dt = x(ρ-z)-y, dz/dt = xy-βz) creates those iconic butterfly-wing patterns. By modulating parameters like σ (Prandtl number), ρ (Rayleigh number), and β, I explore different stability regimes and bifurcation points where the system transitions between ordered and chaotic behavior.
Sacred Geometry & Polygonal Harmonics My mandala and geometric work draws from classical sacred geometry – nested polygons with sides that form harmonic ratios (3, 4, 5, 6, 8, 12), the golden ratio φ = (1+√5)/2, and Fibonacci spirals where each radius relates to the previous by φ. I’m working with rotational symmetry groups and tessellations that have been used for millennia precisely because they resonate with human perception.
Hyperbolic Geometry & Non-Euclidean Space My explorations into hyperbolic tiling (using models like Poincaré disk) create infinite recursive patterns within finite space – the visual mathematics of curved space-time. These M.C. Escher-inspired geometries demonstrate how parallel lines can diverge, creating that sense of infinite depth and altered spatial relationships that supports meditative states.
Modulation & Temporal Dynamics My use of LFOs (Low Frequency Oscillators), clock dividers, and BPM synchronization applies control theory to visual dynamics. I’m essentially creating visual synthesizers where parameters are modulated by sine, triangle, square, or saw waves at musical tempos, creating rhythmic evolution that entrains attention – the mathematical basis of neuromodulation through visual rhythm.
Superposition & Interference Many of my patterns use wave superposition – adding multiple oscillating functions together. Whether it’s multiple Lissajous curves, layered spirals, or overlapping geometric rotations, I’m working with constructive and destructive interference, creating moiré patterns and beat frequencies in visual space.